Uma simples fórmula que desmistifica gráficos 3D

Apresentação

É possível gerar gráficos ‘tridimensionais’ em planos bidimensionais ao brincar com a perspectiva. É mexendo com truques que enganam a percepção humana que softwares conseguem passar a impressão de profundidade.

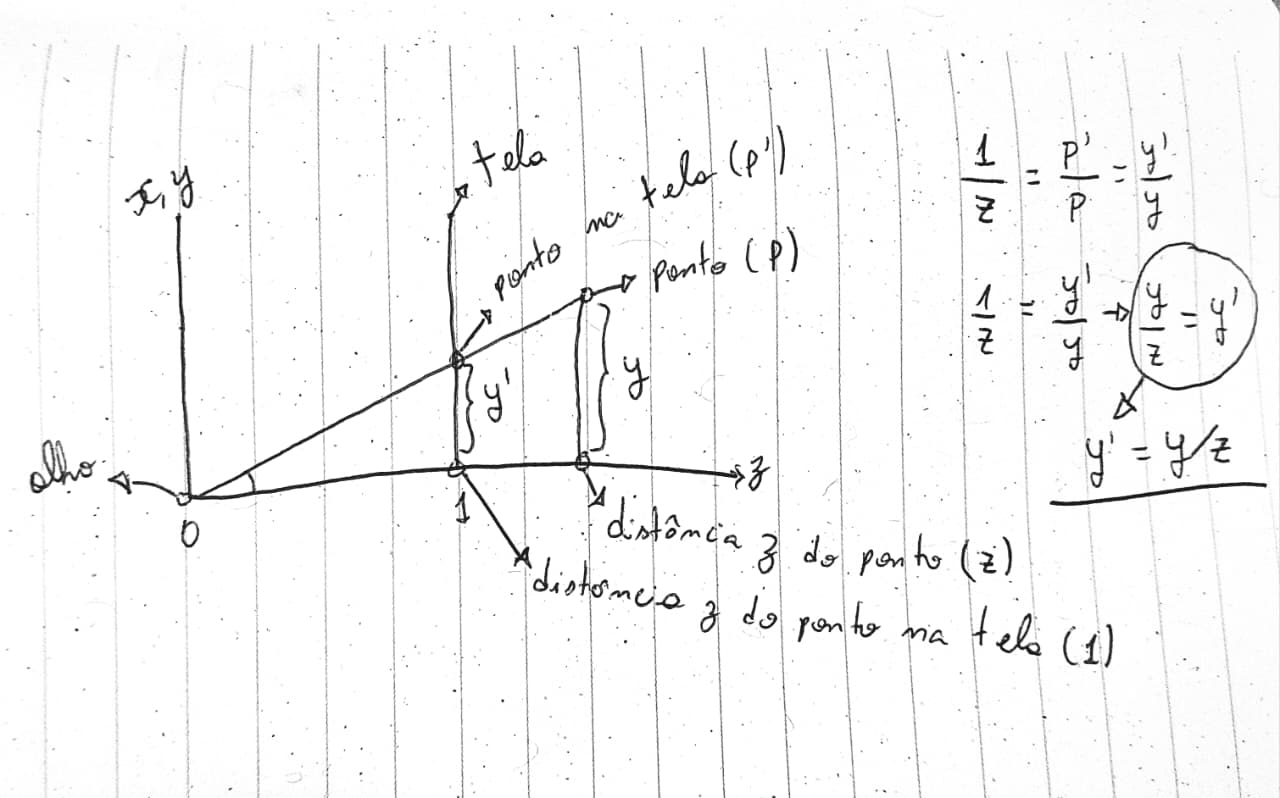
Há uma fórmula muito simples que ajuda a alcançar este feito:

x' = x/z
y' = y/z

Vamos entender?

Imagine um plano bidimensional. Quanto às coordenadas, imagine (0, 0) no meio. Ou seja, no meio do plano, x e y são iguais a zero.

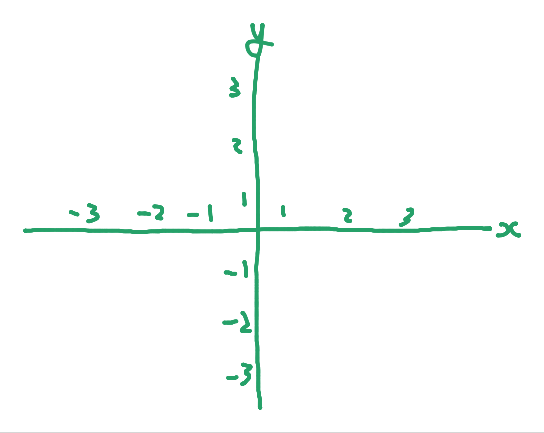
É isso o que representam o x e o y na expressão acima, a posição de um ponto descrita em um plano cartesiano. (3, 3) seria um ponto no topo direito dessa imagem, e (-3, 0) seria um ponto à esquerda, no meio. (0, -3) seria embaixo, no centro.

O z nada mais é do que mais um eixo neste gráfico. Neste caso, seria um de profundidade, indo da frente ao fundo. Aqui, quanto maior o z, mais ao fundo o ponto está.

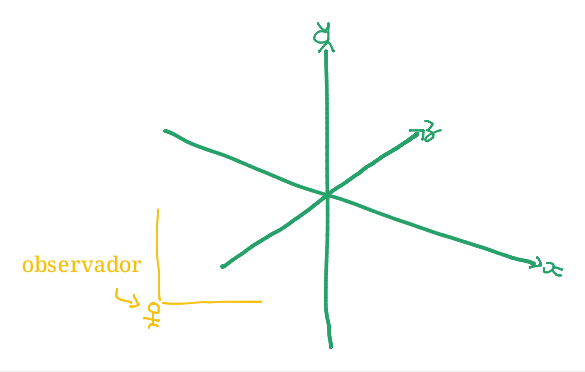
Se quanto mais ao fundo, maior o z, concluímos que:

• quanto mais ao fundo, maior o denominador.

e:

• quanto maior o denominador, menor o resultado.

Isso faz sentido com o mundo real. Olhe através de uma janela e imagine um ponto no topo direito. Agora, imagine que este ponto está se mantendo na mesma altura e na mesma distância horizontal em relação à você, mas está indo para trás.

Ao imaginar esta mesma ação num plano bidimensional, você perceberá que o que ocorre é que:

• o ponto diminui de tamanho, caso você tenha dado a ele um tamanho;
• ele parece se aproximar vertical e horizontalmente em direção à origem, o que é tridimensionalmente apenas uma ilusão de ótica, mas bidimensionalmente uma verdade.

Caso ainda não esteja convencido(a) de que entendeu o que acontece, faça um experimento. Coloque dois objetos em cima de uma mesa, um atrás do outro. Olhando de frente, o segundo objeto estará atrás do primeiro. A partir do momento que você se movimentar para a direita, por exemplo, perceberá que, no seu ponto de vista, o objeto mais atrás estará mais à direita do objeto da frente.

E realmente, se considerarmos que os objetos estão no seu x = -100 (eles estão à esquerda, por isso negativo), a primeira garrafa no z = 10 e a segunda no z = 12.5, vemos que o x' da primeira e da segunda viram:

x' (primeira garrafa) = -100/10 = -10
x'' (segunda garrafa) = -100/12.5 = -8

Ou seja, no nosso plano cartesiano bidimensional, a segunda garrafa estaria mais à direita, pois -8 > -10.

Como garrafas têm tamanho, não são apenas pontos, a segunda garrafa também estaria um pouco menor, por extensão do mesmo princípio. Isso fará mais sentido em breve.

Um detalhe importante

Na tela de um navegador, a origem é definida como o ponto mais acima e mais à esquerda. O eixo x então aumenta para a direita, e o y aumenta para baixo. Esta é a convenção para as janelas. Portanto, devemos mapear os valores corretamente e inverter o eixo vertical.

Qual a intuição?

De maneira intuitiva, soa correto que coisas mais distantes do observador devem se aproximar do centro (pense em montanhas enormes que parecem estar no centro da sua visão, por mais que elas se estendam por quilômetros lado a lado), e que essa razão depende da distância.

Isso também significa que coisas mais distantes parecem se mover mais devagar em relação ao observador, pois qualquer distância efetuada pelo movimento vai ser reduzida pela divisão com a distância (pelo /z da fórmula).

Por que essa fórmula funciona?

A matemática por trás disso é simples e bela. Apenas usamos o fato de que as proporções dos lados de triângulos com os mesmos ângulos serão sempre as mesmas.

Demonstração (código)

Podemos aplicar esta fórmula num contexto 2D e obter uma sensação de profundidade. Veja este simples exemplo em javascript:

<canvas id="game"></canvas>

const BACKGROUND = "#101010";
const FOREGROUND = "#00FF00";

const FPS = 60;


game.width = Math.min(window.screen.width, 800);
game.height = Math.min(window.screen.width, 800);

const ctx = game.getContext("2d");

function clear() {
  ctx.fillStyle = BACKGROUND;
  ctx.fillRect(0, 0, game.width, game.height);
}

function toScreen(p) {
  return {
    x: ((p.x + 1) * game.width) / 2,
    y: ((p.y * -1 + 1) * game.height) / 2,
  };
}

function point({ x, y }) {
  const pointSize = 5;
  ctx.fillStyle = FOREGROUND;
  ctx.fillRect(x - pointSize / 2, y - pointSize / 2, pointSize, pointSize);
}

function line(p1, p2) {
  ctx.strokeStyle = FOREGROUND;
  ctx.beginPath();
  ctx.moveTo(p1.x, p1.y);
  ctx.lineTo(p2.x, p2.y);
  ctx.stroke();
}

function project({ x, y, z }) {
  return {
    x: x / z,
    y: y / z,
  };
}

const vertices = [
  { x: -0.25, y: 0.25, z: 0.25 },
  { x: 0.25, y: 0.25, z: 0.25 },
  { x: 0.25, y: -0.25, z: 0.25 },
  { x: -0.25, y: -0.25, z: 0.25 },

  { x: -0.25, y: 0.25, z: -0.25 },
  { x: 0.25, y: 0.25, z: -0.25 },
  { x: 0.25, y: -0.25, z: -0.25 },
  { x: -0.25, y: -0.25, z: -0.25 },
];

const faces = [
  [0, 1, 2, 3],
  [4, 5, 6, 7],
  [0, 4],
  [1, 5],
  [2, 6],
  [3, 7],
];

function rotate_xz({ x, y, z }, angle) {
  const c = Math.cos(angle);
  const s = Math.sin(angle);
  return {
    x: x * c - z * s,
    y,
    z: x * s + z * c,
  };
}

function translate_z({ x, y, z }, dz) {
  return { x, y, z: z + dz };
}

let dz = 1;
let angle = 0;


function increment_dz(dt) {
  dz += .25 * dt;
}

function decrement_dz(dt) {
  dz -= .25 * dt;
}

let action = increment_dz;

function frame() {
  const dt = 1 / FPS;

  if (dz > 1.4) {
    action = decrement_dz;
  }
  
  if (dz < .4) {
    action = increment_dz;
  }
  
  action(dt);

  angle += Math.PI/3 * dt;
  clear();
  for (const v of vertices) {
    point(toScreen(project(translate_z(rotate_xz(v, angle), dz))));
  }
  for (const f of faces) {
    for (let i = 0; i < f.length; ++i) {
      const a = vertices[f[i]];
      const b = vertices[f[(i + 1) % f.length]];
      line(
        toScreen(project(translate_z(rotate_xz(a, angle), dz))),
        toScreen(project(translate_z(rotate_xz(b, angle), dz))),
      );
    }
  }
  setTimeout(frame, 1000 / FPS);
}
setTimeout(frame, 1000 / FPS);

Demonstração (resultado)

Veja mais

Veja mais sobre isso no vídeo do canal Tsoding (em inglês).